BOND PRICING

Bond Pricing

 

PB =    Price of the bond
Ct =     interest or coupon payments
T     =     number of periods to maturity
r     =     semi-annual discount rate or the semi-annual yield to maturity

Example: Price of 8%, 10-yr. with yield at 6%

Coupon = 4%*1,000 = 40 (Semiannual)
Discount Rate = 3% (Semiannual)
Maturity = 10 years or 20 periods
Par Value = 1,000

BOND CHARACTERISTICS

BOND CHARACTERISTICS

Face or par value
Coupon rate
Zero coupon bond
Compounding and payments
Accrued Interest
Indenture

Treasury Notes and Bonds

T Note maturities range up to 10 years
T bond maturities range from 10 – 30 years
Bid and ask price
Quoted in points  and as a percent of par
Accrued interest
Quoted price does not include interest accrued

Figure 10.1 Listing of Treasury Issues

Corporate Bonds

Most bonds are traded over the counter
Registered
Bearer bonds
Call provisions
Convertible provision
Put provision (putable bonds)
Floating rate bonds
Preferred Stock

Figure 10.2 Investment Grade Bonds

Other Domestic Issuers

Federal Home Loan Bank Board
Farm Credit Agencies
Ginnie Mae
Fannie Mae
Freddie Mac

Innovations in the Bond Market

Reverse floaters
Asset-backed bonds
Pay-in-kind bonds
Catastrophe bonds
Indexed bonds
TIPS (Treasury Inflation Protected Securities)

FACTOR MODELS AND THE ARBITRAGE PRICING THEORY

Arbitrage Pricing Theory

Arbitrage - arises if an investor can construct a zero beta investment portfolio with a return greater than the risk-free rate
If two portfolios are mispriced, the investor could buy the low-priced portfolio and sell the high-priced portfolio
In efficient markets, profitable arbitrage opportunities will quickly disappear

*Note: we will explore more of this with derivatives later

Figure 7.5 Security Line Characteristics

APT and CAPM Compared
APT applies to well diversified portfolios and not necessarily to individual stocks
With APT it is possible for some individual stocks to be mispriced - not lie on the SML
APT is more general in that it gets to an expected return and beta relationship without the assumption of the market portfolio
APT can be extended to multifactor models

THE CAPM AND THE REAL WORLD

CAPM and the Real World

The CAPM was first published by Sharpe in the Journal of Finance in 1964
Many tests of the theory have since followed including Roll’s critique in 1977 and the Fama and French study in 1992

MULTIFACTOR MODELS AND THE CAPM

Multifactor Models

Limitations for CAPM
Market Portfolio is not directly observable
Research shows that other factors affect returns

Fama French Three-Factor Model

Returns are related to factors other than market returns
Size
Book value relative to market value
Three factor model better describes returns

Table 7.3 Summary Statistics for Rates of Return Series

Table 7.4 Regression Statistics for the Single-index and FF Three-factor Model

THE CAPM AND INDEX MODELS

 
Estimating the Index Model
Using historical data on T-bills, S&P 500 and individual securities
Regress risk premiums for individual stocks against the risk premiums for the S&P 500
Slope is the beta for the individual stock

Table 7.1 Monthly Return Statistics for T-bills, S&P 500 and General Motors

Figure 7.3 Cumulative Returns for T-bills, S&P 500 and GM Stock

 Figure 7.4 Characteristic Line for GM

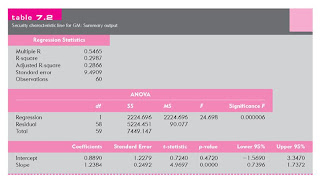
Table 7.2 Security Characteristic Line for GM: Summary Output

 GM Regression:  What We Can Learn

GM is a cyclical stock
Required Return:

rf + b(rm - rf) = 2.75 + 1.24x5.5 = 9.57%

Next compute betas of other firms in the industry

Predicting Betas

The beta from the regression equation is an estimate based on past history
Betas exhibit a statistical property
Regression toward the mean

THE CAPITAL ASSET PRICING MODEL (CAPM)

Capital Asset Pricing Model (CAPM)

What is CAPM?
It is an Equilibrium model that underlies all modern financial theory
CAMP was derived using principles of diversification with simplified assumptions
Markowitz, Sharpe, Lintner and Mossin are researchers credited with its development

Assumptions
Every financial models have key assumption to ease complexity of real worlds.
Of course there are pros and cons with those assumptions.
CAPM makes a number of assumption,

-Individual investors are price takers
-Single-period investment horizon
-Investments are limited to traded financial assets
-No taxes nor transaction costs
-Information is costless and available to all investors
-Investors are rational mean-variance optimizers
-Homogeneous expectations

Resulting Equilibrium Conditions

All investors will hold the same portfolio for risky assets – market portfolio
Market portfolio contains all securities and the proportion of each security is its market value as a percentage of total market value
Risk premium on the market depends on the average risk aversion of all market participants
Risk premium on an individual security is a function of its covariance with the market

Figure 7.1 The Efficient Frontier and the Capital Market Line

The Risk Premium of the Market Portfolio

M    =    Market portfolio    
rf    =    Risk free rate    
E(rM) - rf    =    Market risk premium    
E(rM) - rf   / sim =    Market price of risk = Slope of the CAPM

*sim = sigma (std. deviation) of market

Expected Returns On Individual Securities

The risk premium on individual securities is a function of the individual security’s contribution to the risk of the market portfolio
Individual security’s risk premium is a function of the covariance of returns with the assets that make up the market portfolio

Expected Returns On Individual Securities: an Example 

Using the Dell example from previous post:

(E(rm) - rf) / 1 = (E(rd) - rf) / Bd

Rearranging gives us the CAPM’s expected return-beta relationship

E(rd) = rf + Bd [E(rm) - rf)]

Figure 7.2 The Security Market Line and Positive Alpha Stock

SML Relationships

b =     [COV(ri,rm)] / sm2
E(rm) – rf   =     market risk premium
SML = rf + b[E(rm) - rf]





Sample Calculations for SML

E(rm) - rf = .08    rf = .03

bx = 1.25
    E(rx) = .03 + 1.25(.08) = .13 or 13%

by = .6
    e(ry) = .03 + .6(.08) = .078 or 7.8%

Graph of Sample Calculations

RISK OF LONG-TERM INVESTMENTS

Are Stock Returns Less Risky in the Long Run?

Consider a 2-year investment

Variance of the 2-year return is double of that of the one-year return and σ is higher by a multiple of the square root of 2

Generalizing to an investment horizon of n years and then annualizing:

The Fly in the ‘Time Diversification’ Ointment

Annualized standard deviation is only appropriate for short-term portfolios
Variance grows linearly with the number of years
Standard deviation grows in proportion to

To compare investments in two different time periods:
-Risk of the total (end of horizon) rate of return
-Accounts for magnitudes and probabilities