BOND CHARACTERISTICS
Face or par value
Coupon rate
Zero coupon bond
Compounding and payments
Accrued Interest
Indenture
Treasury Notes and Bonds
T Note maturities range up to 10 years
T bond maturities range from 10 – 30 years
Bid and ask price
Quoted in points and as a percent of par
Accrued interest
Quoted price does not include interest accrued
Figure 10.1 Listing of Treasury Issues
Corporate Bonds
Most bonds are traded over the counter
Registered
Bearer bonds
Call provisions
Convertible provision
Put provision (putable bonds)
Floating rate bonds
Preferred Stock
Figure 10.2 Investment Grade Bonds
Other Domestic Issuers
Federal Home Loan Bank Board
Farm Credit Agencies
Ginnie Mae
Fannie Mae
Freddie Mac
Innovations in the Bond Market
Reverse floaters
Asset-backed bonds
Pay-in-kind bonds
Catastrophe bonds
Indexed bonds
TIPS (Treasury Inflation Protected Securities)
This blog is for myself and all others who want to learn about financial investment in general. While the focus of blog is on stocks, I would also like to cover: bond, derivative (options, swaps, future and forward), fund, currency, commodity, Treasury bill (risk-free)/bond, speculation, hedge, black-scholes
Sunday, September 19, 2010
Friday, September 17, 2010
FACTOR MODELS AND THE ARBITRAGE PRICING THEORY
Arbitrage Pricing Theory
Arbitrage - arises if an investor can construct a zero beta investment portfolio with a return greater than the risk-free rate
If two portfolios are mispriced, the investor could buy the low-priced portfolio and sell the high-priced portfolio
In efficient markets, profitable arbitrage opportunities will quickly disappear
*Note: we will explore more of this with derivatives later
Figure 7.5 Security Line Characteristics
APT and CAPM Compared
APT applies to well diversified portfolios and not necessarily to individual stocks
With APT it is possible for some individual stocks to be mispriced - not lie on the SML
APT is more general in that it gets to an expected return and beta relationship without the assumption of the market portfolio
APT can be extended to multifactor models
Arbitrage - arises if an investor can construct a zero beta investment portfolio with a return greater than the risk-free rate
If two portfolios are mispriced, the investor could buy the low-priced portfolio and sell the high-priced portfolio
In efficient markets, profitable arbitrage opportunities will quickly disappear
*Note: we will explore more of this with derivatives later
Figure 7.5 Security Line Characteristics
APT and CAPM Compared
APT applies to well diversified portfolios and not necessarily to individual stocks
With APT it is possible for some individual stocks to be mispriced - not lie on the SML
APT is more general in that it gets to an expected return and beta relationship without the assumption of the market portfolio
APT can be extended to multifactor models
THE CAPM AND THE REAL WORLD
CAPM and the Real World
The CAPM was first published by Sharpe in the Journal of Finance in 1964
Many tests of the theory have since followed including Roll’s critique in 1977 and the Fama and French study in 1992
MULTIFACTOR MODELS AND THE CAPM
Multifactor Models
Limitations for CAPM
Market Portfolio is not directly observable
Research shows that other factors affect returns
Fama French Three-Factor Model
Returns are related to factors other than market returns
Size
Book value relative to market value
Three factor model better describes returns
Table 7.3 Summary Statistics for Rates of Return Series
Table 7.4 Regression Statistics for the Single-index and FF Three-factor Model
The CAPM was first published by Sharpe in the Journal of Finance in 1964
Many tests of the theory have since followed including Roll’s critique in 1977 and the Fama and French study in 1992
MULTIFACTOR MODELS AND THE CAPM
Multifactor Models
Limitations for CAPM
Market Portfolio is not directly observable
Research shows that other factors affect returns
Fama French Three-Factor Model
Returns are related to factors other than market returns
Size
Book value relative to market value
Three factor model better describes returns
Table 7.3 Summary Statistics for Rates of Return Series
Table 7.4 Regression Statistics for the Single-index and FF Three-factor Model
THE CAPM AND INDEX MODELS
Estimating the Index Model
Using historical data on T-bills, S&P 500 and individual securities
Regress risk premiums for individual stocks against the risk premiums for the S&P 500
Slope is the beta for the individual stock
Table 7.1 Monthly Return Statistics for T-bills, S&P 500 and General Motors
Figure 7.3 Cumulative Returns for T-bills, S&P 500 and GM Stock
Figure 7.4 Characteristic Line for GM
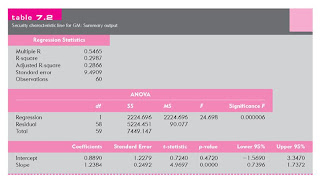
Table 7.2 Security Characteristic Line for GM: Summary Output
GM Regression: What We Can Learn
GM is a cyclical stock
Required Return:
rf + b(rm - rf) = 2.75 + 1.24x5.5 = 9.57%
Next compute betas of other firms in the industry
Predicting Betas
The beta from the regression equation is an estimate based on past history
Betas exhibit a statistical property
Regression toward the mean
Saturday, September 11, 2010
THE CAPITAL ASSET PRICING MODEL (CAPM)
Capital Asset Pricing Model (CAPM)
What is CAPM?
It is an Equilibrium model that underlies all modern financial theory
CAMP was derived using principles of diversification with simplified assumptions
Markowitz, Sharpe, Lintner and Mossin are researchers credited with its development
Assumptions
Every financial models have key assumption to ease complexity of real worlds.
Of course there are pros and cons with those assumptions.
CAPM makes a number of assumption,
-Individual investors are price takers
-Single-period investment horizon
-Investments are limited to traded financial assets
-No taxes nor transaction costs
-Information is costless and available to all investors
-Investors are rational mean-variance optimizers
-Homogeneous expectations
Resulting Equilibrium Conditions
All investors will hold the same portfolio for risky assets – market portfolio
Market portfolio contains all securities and the proportion of each security is its market value as a percentage of total market value
Risk premium on the market depends on the average risk aversion of all market participants
Risk premium on an individual security is a function of its covariance with the market
Figure 7.1 The Efficient Frontier and the Capital Market Line
The Risk Premium of the Market Portfolio
M = Market portfolio
rf = Risk free rate
E(rM) - rf = Market risk premium
E(rM) - rf / sim = Market price of risk = Slope of the CAPM
*sim = sigma (std. deviation) of market
Expected Returns On Individual Securities
The risk premium on individual securities is a function of the individual security’s contribution to the risk of the market portfolio
Individual security’s risk premium is a function of the covariance of returns with the assets that make up the market portfolio
Expected Returns On Individual Securities: an Example
Using the Dell example from previous post:
(E(rm) - rf) / 1 = (E(rd) - rf) / Bd
Rearranging gives us the CAPM’s expected return-beta relationship
E(rd) = rf + Bd [E(rm) - rf)]
Figure 7.2 The Security Market Line and Positive Alpha Stock
SML Relationships
b = [COV(ri,rm)] / sm2
E(rm) – rf = market risk premium
SML = rf + b[E(rm) - rf]
Sample Calculations for SML
E(rm) - rf = .08 rf = .03
bx = 1.25
E(rx) = .03 + 1.25(.08) = .13 or 13%
by = .6
e(ry) = .03 + .6(.08) = .078 or 7.8%
Graph of Sample Calculations
What is CAPM?
It is an Equilibrium model that underlies all modern financial theory
CAMP was derived using principles of diversification with simplified assumptions
Markowitz, Sharpe, Lintner and Mossin are researchers credited with its development
Assumptions
Every financial models have key assumption to ease complexity of real worlds.
Of course there are pros and cons with those assumptions.
CAPM makes a number of assumption,
-Individual investors are price takers
-Single-period investment horizon
-Investments are limited to traded financial assets
-No taxes nor transaction costs
-Information is costless and available to all investors
-Investors are rational mean-variance optimizers
-Homogeneous expectations
Resulting Equilibrium Conditions
All investors will hold the same portfolio for risky assets – market portfolio
Market portfolio contains all securities and the proportion of each security is its market value as a percentage of total market value
Risk premium on the market depends on the average risk aversion of all market participants
Risk premium on an individual security is a function of its covariance with the market
Figure 7.1 The Efficient Frontier and the Capital Market Line
The Risk Premium of the Market Portfolio
M = Market portfolio
rf = Risk free rate
E(rM) - rf = Market risk premium
E(rM) - rf / sim = Market price of risk = Slope of the CAPM
*sim = sigma (std. deviation) of market
Expected Returns On Individual Securities
The risk premium on individual securities is a function of the individual security’s contribution to the risk of the market portfolio
Individual security’s risk premium is a function of the covariance of returns with the assets that make up the market portfolio
Expected Returns On Individual Securities: an Example
Using the Dell example from previous post:
(E(rm) - rf) / 1 = (E(rd) - rf) / Bd
Rearranging gives us the CAPM’s expected return-beta relationship
E(rd) = rf + Bd [E(rm) - rf)]
Figure 7.2 The Security Market Line and Positive Alpha Stock
SML Relationships
b = [COV(ri,rm)] / sm2
E(rm) – rf = market risk premium
SML = rf + b[E(rm) - rf]
Sample Calculations for SML
E(rm) - rf = .08 rf = .03
bx = 1.25
E(rx) = .03 + 1.25(.08) = .13 or 13%
by = .6
e(ry) = .03 + .6(.08) = .078 or 7.8%
Graph of Sample Calculations
Thursday, September 9, 2010
RISK OF LONG-TERM INVESTMENTS
Are Stock Returns Less Risky in the Long Run?
Consider a 2-year investment
Variance of the 2-year return is double of that of the one-year return and σ is higher by a multiple of the square root of 2
Generalizing to an investment horizon of n years and then annualizing:
The Fly in the ‘Time Diversification’ Ointment
Annualized standard deviation is only appropriate for short-term portfolios
Variance grows linearly with the number of years
Standard deviation grows in proportion to
To compare investments in two different time periods:
-Risk of the total (end of horizon) rate of return
-Accounts for magnitudes and probabilities
Consider a 2-year investment
Variance of the 2-year return is double of that of the one-year return and σ is higher by a multiple of the square root of 2
Generalizing to an investment horizon of n years and then annualizing:
The Fly in the ‘Time Diversification’ Ointment
Annualized standard deviation is only appropriate for short-term portfolios
Variance grows linearly with the number of years
Standard deviation grows in proportion to
To compare investments in two different time periods:
-Risk of the total (end of horizon) rate of return
-Accounts for magnitudes and probabilities
A SINGLE-FACTOR ASSET MARKET
Single Factor Model
βi = index of a securities’ particular return to the factor
M = unanticipated movement commonly related to security returns
Ei = unexpected event relevant only to this security
Assumption: a broad market index like the S&P500 is the common factor
Specification of a Single-Index Model of Security Returns
Use the S&P 500 as a market proxy
Excess return can now be stated as:
This specifies the both market and firm risk
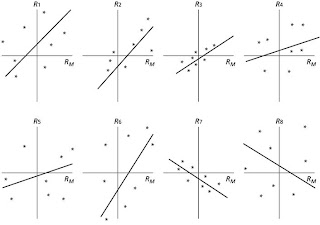
Figure 6.11 Scatter Diagram for Dell
Figure 6.12 Various Scatter Diagrams
Components of Risk
Market or systematic risk: risk related to the macro economic factor or market index
Unsystematic or firm specific risk: risk not related to the macro factor or market index
Total risk = Systematic + Unsystematic
Measuring Components of Risk
si2 = bi2 sm2 + s2(ei)
where;
si2 = total variance
bi2 sm2 = systematic variance
s2(ei) = unsystematic variance
*s=std. deviation
Examining Percentage of Variance
Total Risk = Systematic Risk + Unsystematic Risk
Systematic Risk/Total Risk = p2
ßi2 s m2 / s2 = p2
bi2 sm2 / bi2 sm2 + s2(ei) = p2
Advantages of the Single Index Model
Reduces the number of inputs for diversification
Easier for security analysts to specialize
βi = index of a securities’ particular return to the factor
M = unanticipated movement commonly related to security returns
Ei = unexpected event relevant only to this security
Assumption: a broad market index like the S&P500 is the common factor
Specification of a Single-Index Model of Security Returns
Use the S&P 500 as a market proxy
Excess return can now be stated as:
This specifies the both market and firm risk
Figure 6.11 Scatter Diagram for Dell
Figure 6.12 Various Scatter Diagrams
Components of Risk
Market or systematic risk: risk related to the macro economic factor or market index
Unsystematic or firm specific risk: risk not related to the macro factor or market index
Total risk = Systematic + Unsystematic
Measuring Components of Risk
si2 = bi2 sm2 + s2(ei)
where;
si2 = total variance
bi2 sm2 = systematic variance
s2(ei) = unsystematic variance
*s=std. deviation
Examining Percentage of Variance
Total Risk = Systematic Risk + Unsystematic Risk
Systematic Risk/Total Risk = p2
ßi2 s m2 / s2 = p2
bi2 sm2 / bi2 sm2 + s2(ei) = p2
Advantages of the Single Index Model
Reduces the number of inputs for diversification
Easier for security analysts to specialize
Monday, September 6, 2010
EFFICIENT DIVERSIFICATION WITH MANY RISKY ASSETS
Extending Concepts to All Securities
-The optimal combinations result in lowest level of risk for a given return
-The optimal trade-off is described as the efficient frontier
-These portfolios are dominant
Portfolios Constructed from Three Stocks A, B and C
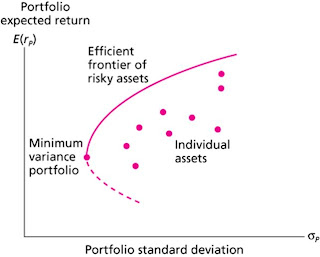
The Efficient Frontier of Risky Assets and Individual Assets
This graph shows nothing more than an optimal choice.
Given the risk, you will pick the point along the efficient frontier which gives the maximized E(r).
-The optimal combinations result in lowest level of risk for a given return
-The optimal trade-off is described as the efficient frontier
-These portfolios are dominant
Portfolios Constructed from Three Stocks A, B and C
The Efficient Frontier of Risky Assets and Individual Assets
This graph shows nothing more than an optimal choice.
Given the risk, you will pick the point along the efficient frontier which gives the maximized E(r).
THE OPTIMAL RISKY PORTFOLIO WITH A RISK-FREE ASSET
Instead of two risky assets (bond and stock), we can compose a portfolio with one risky and one risk free assets.
Extending to Include Riskless Asset
-The optimal combination becomes linear
-A single combination of risky and riskless assets will dominate
Figure: Opportunity Set Using Stocks and Bonds and Two Capital Allocation Lines
Dominant CAL with a Risk-Free Investment (F)
CAL(O) dominates other lines -- it has the best risk/return or the largest slope
Slope = [ E(ra)-rf ] / std. dev
[ E(rp) - rf ] / std. dev. p > [ E(ra) - rf ] / std. dev.a
Regardless of risk preferences, combinations of O & F dominate
Optimal Capital Allocation Line for Bonds, Stocks and T-Bills
The Complete Portfolio
The Complete Portfolio – Solution to the Asset Allocation Problem
Instead of two risky assets (bond and stock), we can compose a portfolio with one risky and one risk free assets.
Extending to Include Riskless Asset
-The optimal combination becomes linear
-A single combination of risky and riskless assets will dominate
Figure: Opportunity Set Using Stocks and Bonds and Two Capital Allocation Lines
Dominant CAL with a Risk-Free Investment (F)
CAL(O) dominates other lines -- it has the best risk/return or the largest slope
Slope = [ E(ra)-rf ] / std. dev
[ E(rp) - rf ] / std. dev. p > [ E(ra) - rf ] / std. dev.a
Regardless of risk preferences, combinations of O & F dominate
Optimal Capital Allocation Line for Bonds, Stocks and T-Bills
The Complete Portfolio
The Complete Portfolio – Solution to the Asset Allocation Problem
Saturday, September 4, 2010
ASSET ALLOCATION WITH TWO RISKY ASSETS
Covariance and Correlation
-Portfolio risk depends on the correlation between the returns of the assets in the portfolio
-Covariance and the correlation coefficient provide a measure of the returns on two assets to vary
Two Asset Portfolio Return – Stock and Bond
Covariance and Correlation Coefficient
Correlation Coefficients: Possible Values
Range of values for r 1,2
-1.0 < r < 1.0
If r = 1.0, the securities would be perfectly positively correlated (meaning two assets move in the same direction)
If r = - 1.0, the securities would be perfectly negatively correlated (meaning two assets move in the opposite direction)
Two Asset Portfolio St Dev – Stock and Bond
In General, For an n-Security Portfolio:
rp = Weighted average of the
n securities
sp2 = (Consider all pair-wise
covariance measures)
Three Rules of Two-Risky-Asset Portfolios
Numerical Example: Bond and Stock Returns
Returns
Bond = 6% Stock = 10%
Standard Deviation
Bond = 12% Stock = 25%
Weights
Bond = .5 Stock = .5
Correlation Coefficient
(Bonds and Stock) = 0
Return = 8%
.5(6) + .5 (10)
Standard Deviation = 13.87%
[(.5)^2 (12)^2 + (.5)^2 (25)^2 + …
2 (.5) (.5) (12) (25) (0)]^ ½
[192.25]^ ½ = 13.87
Investment Opportunity Set for Stocks and Bonds
Investment Opportunity Set for Stocks and Bonds with Various Correlations
-Portfolio risk depends on the correlation between the returns of the assets in the portfolio
-Covariance and the correlation coefficient provide a measure of the returns on two assets to vary
Two Asset Portfolio Return – Stock and Bond
Covariance and Correlation Coefficient
Correlation Coefficients: Possible Values
Range of values for r 1,2
-1.0 < r < 1.0
If r = 1.0, the securities would be perfectly positively correlated (meaning two assets move in the same direction)
If r = - 1.0, the securities would be perfectly negatively correlated (meaning two assets move in the opposite direction)
Two Asset Portfolio St Dev – Stock and Bond
In General, For an n-Security Portfolio:
rp = Weighted average of the
n securities
sp2 = (Consider all pair-wise
covariance measures)
Three Rules of Two-Risky-Asset Portfolios
Numerical Example: Bond and Stock Returns
Returns
Bond = 6% Stock = 10%
Standard Deviation
Bond = 12% Stock = 25%
Weights
Bond = .5 Stock = .5
Correlation Coefficient
(Bonds and Stock) = 0
Return = 8%
.5(6) + .5 (10)
Standard Deviation = 13.87%
[(.5)^2 (12)^2 + (.5)^2 (25)^2 + …
2 (.5) (.5) (12) (25) (0)]^ ½
[192.25]^ ½ = 13.87
Investment Opportunity Set for Stocks and Bonds
Investment Opportunity Set for Stocks and Bonds with Various Correlations
DIVERSIFICATION AND PORTFOLIO RISK
Diversification means reducing risk by investing in a variety of assets. In other words, you are spreading risks among assets. There are two different types of risk in investment.
1. Market risk
-Systematic or Nondiversifiable
2. Firm-specific risk
-Diversifiable or nonsystematic
Market risk is systematic and everyone involved in market must bear it. On the other hand, firm specific can be diversified to some degree.
Here's a figure showing Portfolio Risk as a Function of the Number of Stocks.
As you can see on the B, market risk is fixed at some level and firm-specific adds up.
Portfolio Risk as a Function of Number of Securities
A graph above illustrates that risk (std deviation) declines as the number of stocks in a portfolio increases.
1. Market risk
-Systematic or Nondiversifiable
2. Firm-specific risk
-Diversifiable or nonsystematic
Market risk is systematic and everyone involved in market must bear it. On the other hand, firm specific can be diversified to some degree.
Here's a figure showing Portfolio Risk as a Function of the Number of Stocks.
As you can see on the B, market risk is fixed at some level and firm-specific adds up.
Portfolio Risk as a Function of Number of Securities
A graph above illustrates that risk (std deviation) declines as the number of stocks in a portfolio increases.
Thursday, September 2, 2010
PASSIVE STRATEGIES AND THE CAPITAL MARKET LINE
Average Rates of Return, Standard Deviation and Reward to Variability
Costs and Benefits of Passive Investing
1. Active strategy entails costs: If you pick active strategy, you need constant flow of updated information. This can be very costly. In addition to that, you keep the track of your stocks every hour, minute or even second. Monitoring every movement is time consuming and may need a bunch of staff members to do so. On top of that, you must adapt to changing environment whether it is an external or internal and reevaluate your stocks accordingly.
2. Free-rider benefit
3. Involves investment in two passive portfolios
-Short-term T-bills
-Fund of common stocks that mimics a broad market index
Costs and Benefits of Passive Investing
1. Active strategy entails costs: If you pick active strategy, you need constant flow of updated information. This can be very costly. In addition to that, you keep the track of your stocks every hour, minute or even second. Monitoring every movement is time consuming and may need a bunch of staff members to do so. On top of that, you must adapt to changing environment whether it is an external or internal and reevaluate your stocks accordingly.
2. Free-rider benefit
3. Involves investment in two passive portfolios
-Short-term T-bills
-Fund of common stocks that mimics a broad market index
ASSET ALLOCATION ACROSS RISKY AND RISK-FREE PORTFOLIOS
Allocating Capital
1. Possible to split investment funds between safe and risky assets
2. Risk free asset: proxy; T-bills
3. Risky asset: stock (or a portfolio)
Issues to consider
1. Examine risk/ return tradeoff
2. Demonstrate how different degrees of risk aversion will affect allocations between risky and risk free assets
Example
Total portfolio value = $300,000
Risk-free value = 90,000
Risky (Vanguard and Fidelity) = 210,000
Vanguard (V) = 54%
Fidelity (F) = 46%
CALCULATING EXPECTED RETURN
rf = 7%
srf = 0% (std. dev of risk free)
E(rp) = 15%
sp = 22% (std. dev of portfolio)
y = % in p (risky)
(1-y) = % in rf
E(rc) = yE(rp) + (1 - y)rf
rc = complete or combined portfolio
For example, y = .75
E(rc) = .75(.15) + .25(.07)
= .13 or 13%
Investment Opportunity Set with a Risk-Free Investment
Variance on the Possible Combined Portfolios: Since srf = 0 then sc = y*sp
What it means is that standard deviation of risk free asset = 0. So only variance/std deviation that we should be concerned is risky asset/portfolio. Multiply std deviation of risky asset by the asset's allocation % to get total std. deviation.
Combinations Without Leverage
If y = .75, then
sc = .75(.22) = .165 or 16.5%
If y = 1
sc = 1(.22) = .22 or 22%
If y = 0
sc = 0(.22) = .00 or 0%
Using Leverage with Capital Allocation Line
Borrow at the Risk-Free Rate and invest in stock
Using 50% Leverage
rc = (-.5) (.07) + (1.5) (.15) = .19
sc = (1.5) (.22) = .33
Risk Aversion and Allocation
1. Greater levels of risk aversion lead to larger proportions of the risk free rate
2. Lower levels of risk aversion lead to larger proportions of the portfolio of risky assets
3. Willingness to accept high levels of risk for high levels of returns would result in leveraged combinations
1. Possible to split investment funds between safe and risky assets
2. Risk free asset: proxy; T-bills
3. Risky asset: stock (or a portfolio)
Issues to consider
1. Examine risk/ return tradeoff
2. Demonstrate how different degrees of risk aversion will affect allocations between risky and risk free assets
Example
Total portfolio value = $300,000
Risk-free value = 90,000
Risky (Vanguard and Fidelity) = 210,000
Vanguard (V) = 54%
Fidelity (F) = 46%
CALCULATING EXPECTED RETURN
rf = 7%
srf = 0% (std. dev of risk free)
E(rp) = 15%
sp = 22% (std. dev of portfolio)
y = % in p (risky)
(1-y) = % in rf
E(rc) = yE(rp) + (1 - y)rf
rc = complete or combined portfolio
For example, y = .75
E(rc) = .75(.15) + .25(.07)
= .13 or 13%
Investment Opportunity Set with a Risk-Free Investment
Variance on the Possible Combined Portfolios: Since srf = 0 then sc = y*sp
What it means is that standard deviation of risk free asset = 0. So only variance/std deviation that we should be concerned is risky asset/portfolio. Multiply std deviation of risky asset by the asset's allocation % to get total std. deviation.
Combinations Without Leverage
If y = .75, then
sc = .75(.22) = .165 or 16.5%
If y = 1
sc = 1(.22) = .22 or 22%
If y = 0
sc = 0(.22) = .00 or 0%
Using Leverage with Capital Allocation Line
Borrow at the Risk-Free Rate and invest in stock
Using 50% Leverage
rc = (-.5) (.07) + (1.5) (.15) = .19
sc = (1.5) (.22) = .33
Risk Aversion and Allocation
1. Greater levels of risk aversion lead to larger proportions of the risk free rate
2. Lower levels of risk aversion lead to larger proportions of the portfolio of risky assets
3. Willingness to accept high levels of risk for high levels of returns would result in leveraged combinations
INFLATION AND REAL RATES OF RETURN
Real vs. Nominal Rates
It is an important element to consider in an investment. Unfortunately many people ignore real value of their returns and exclusively focus on nominal value. For instance, your t-bill yielded 3.5% last year but inflation rate for the year was 4%. A dollar invested in the t-bill became $1.035. That sure is increase in nominal value but are you truly better off? Well, no. Because after the inflation, you actually incurred a loss of 0.5%. Compared to last year, you have less purchasing power.
As a shrewd investor, you must take inflation into account and compute real rate of return.
Fisher effect: Approximation
nominal rate = real rate + inflation premium
Note that this is only an approximation and not an accurate formula but it is close enough. So no further complex computation is not needed.
R = r + i or r = R - i
R = nominal and r = real
Example r = 3%, i = 6%
R = 9% = 3% + 6% or 3% = 9% - 6%
It is an important element to consider in an investment. Unfortunately many people ignore real value of their returns and exclusively focus on nominal value. For instance, your t-bill yielded 3.5% last year but inflation rate for the year was 4%. A dollar invested in the t-bill became $1.035. That sure is increase in nominal value but are you truly better off? Well, no. Because after the inflation, you actually incurred a loss of 0.5%. Compared to last year, you have less purchasing power.
As a shrewd investor, you must take inflation into account and compute real rate of return.
Fisher effect: Approximation
nominal rate = real rate + inflation premium
Note that this is only an approximation and not an accurate formula but it is close enough. So no further complex computation is not needed.
R = r + i or r = R - i
R = nominal and r = real
Example r = 3%, i = 6%
R = 9% = 3% + 6% or 3% = 9% - 6%
Wednesday, September 1, 2010
Risk Premiums and Risk Aversion
Risk level of an investor is determined by degree to which investors are willing to commit funds
Risk aversion is how reluctant you are in investing.
If T-Bill denotes the risk-free rate, rf, and variance denotes volatility of returns then:
The risk premium of a portfolio is: E(rp) - rf
In other words, expected return of portfolio minus risk-free rate.
To quantify the degree of risk aversion with parameter A:
The Sharpe (Reward-to-Volatility) Measure
This sharpe ratio is known to be used by mutual/hedge fund managers. This shows how much extra/additional return (excessive return or premium) you are earning when you bear a unit of risk in an investment. The Sharpe ratio has as its principal advantage that it is directly computable from any observed series of returns without need for additional information surrounding the source of profitability.
Risk aversion is how reluctant you are in investing.
If T-Bill denotes the risk-free rate, rf, and variance denotes volatility of returns then:
The risk premium of a portfolio is: E(rp) - rf
In other words, expected return of portfolio minus risk-free rate.
To quantify the degree of risk aversion with parameter A:
The Sharpe (Reward-to-Volatility) Measure
This sharpe ratio is known to be used by mutual/hedge fund managers. This shows how much extra/additional return (excessive return or premium) you are earning when you bear a unit of risk in an investment. The Sharpe ratio has as its principal advantage that it is directly computable from any observed series of returns without need for additional information surrounding the source of profitability.
Risk and risk premium
Risk is uncertainty. When you make an investment, there is always a risk associated with it whether it is a bond, stock, fund, etc. Risk arises from uncertainty. We don't know market direction next year. As a matter of fact, we don't even know how market will drop/raise our stock price tomorrow. Risk can be separated into 2 different types. One is an internal risk. This is also known as a business specific risk, where uncertainty comes from the company and its operation. The other one is a market risk. This is an external risk that you will have to bear.
Scenario Analysis and Probability Distributions
In order to examine risk, we can look at the risk/uncertainty using probability. Here 3 important variables that you need to know before moving on the analysis.
1) Mean: most likely value
2) Variance or standard deviation
3) Skewness
This picture demonstrates famous concept known as "normal distribution." The normal distribution is an absolutely continuous probability distribution whose cumulants of all orders above two are zero. Note that norm. distribution has mean equals to median.
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. skewness value can be positive or negative, or even undefined. Qualitatively, a negative skew indicates that the tail on the left side of probability density function is longer than the right side and the bulk of the values (including the median) lie to the right of the mean. A positive skew indicates that the tail on the right side is longer than the left side and the bulk of the values lie to the left of the mean.
Measuring Mean: Scenario or Subjective Returns
p(s) = probability of a state
r(s) = return if a state occurs
1 to s states
This is a formula to calculate expected return (subjective/scenario return), which is equals to multiplication of each state's probability (in decimal) and return. After you get each value, sum them up to get final E(r) value.
Numerical Example: Subjective or Scenario Distributions
State Prob. of State rin State
1 .1 -.05
2 .2 .05
3 .4 .15
4 .2 .25
5 .1 .35
E(r) = (.1)(-.05) + (.2)(.05)...+ (.1)(.35)
E(r) = .15 or 15%
Measuring Variance or Dispersion of Returns
Variance is used as one of several descriptors of a distribution. It describes how far values lie from the mean.
Var = sum of probability (in decimal) multiplied by outcome of individual return minus average. And Standard deviation is simply a square root of variance.
Using the same example above,
Var =[(.1)(-.05-.15)2+(.2)(.05- .15)2...+ .1(.35-.15)2]
Var= .01199
S.D.= [ .01199] 1/2 = .1095 or 10.95%
Scenario Analysis and Probability Distributions
In order to examine risk, we can look at the risk/uncertainty using probability. Here 3 important variables that you need to know before moving on the analysis.
1) Mean: most likely value
2) Variance or standard deviation
3) Skewness
This picture demonstrates famous concept known as "normal distribution." The normal distribution is an absolutely continuous probability distribution whose cumulants of all orders above two are zero. Note that norm. distribution has mean equals to median.
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. skewness value can be positive or negative, or even undefined. Qualitatively, a negative skew indicates that the tail on the left side of probability density function is longer than the right side and the bulk of the values (including the median) lie to the right of the mean. A positive skew indicates that the tail on the right side is longer than the left side and the bulk of the values lie to the left of the mean.
Measuring Mean: Scenario or Subjective Returns
p(s) = probability of a state
r(s) = return if a state occurs
1 to s states
This is a formula to calculate expected return (subjective/scenario return), which is equals to multiplication of each state's probability (in decimal) and return. After you get each value, sum them up to get final E(r) value.
Numerical Example: Subjective or Scenario Distributions
State Prob. of State rin State
1 .1 -.05
2 .2 .05
3 .4 .15
4 .2 .25
5 .1 .35
E(r) = (.1)(-.05) + (.2)(.05)...+ (.1)(.35)
E(r) = .15 or 15%
Measuring Variance or Dispersion of Returns
Variance is used as one of several descriptors of a distribution. It describes how far values lie from the mean.
Var = sum of probability (in decimal) multiplied by outcome of individual return minus average. And Standard deviation is simply a square root of variance.
Using the same example above,
Var =[(.1)(-.05-.15)2+(.2)(.05- .15)2...+ .1(.35-.15)2]
Var= .01199
S.D.= [ .01199] 1/2 = .1095 or 10.95%
Subscribe to:
Comments (Atom)